Answer:
If f(-x) = f(x), f is even and is symmetric about y
If f(-x) = -f(x), f is odd and is symmetric about the origin
If
 and
and
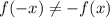 , f is neither even nor odd and does not have symmetry
, f is neither even nor odd and does not have symmetry
Explanation:
As we discussed in one of the previous questions, if f(-x) = f(x), we have an even function. One basic example of an even function is x^2 since (-x)^2 = x^2. On the other hand, if f(-x) = -f(x), we have an odd function. One common example is x^3 since (-x)^3 = -x^3. What we have not been over yet is the symmetry of the functions. In order to do this, let's examine x^2 and x^3. x^2, which is an even function, is symmetric to the y-axis. The graph is a parabola that looks exactly the same on the left and the right of the y-axis.
On the other hand, x^3, which is an odd function, is not symmetric to the y-axis. On the other hand, it is symmetric to the origin. You can imagine that if you flipped y = x^3 across the origin, you would end up getting a graph that looks exactly the same.
A function that is neither even nor odd, meaning
 and
and
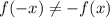 , one that is not odd or even, has no symmetry. It is not symmetric about the y-axis or the origin.
, one that is not odd or even, has no symmetry. It is not symmetric about the y-axis or the origin.