We know for a fact that the equation: |z+z'| \leqslant |z|+|z'| holds for any 2 complex numbers I came up with the conclusion that: |z+z'|=|z|+|z'|only holds…

Question

We know for a fact that the equation:


`|z+z'| \leqslant |z|+|z'|`
holds for any 2 complex numbers

I came up with the conclusion that:

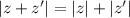
`|z+z'|=|z|+|z'|`only holds when z and z' are pure imaginary or pure real numbers of the SAME sign.
How can i prove this algebraically/geometrically?
Note: Irrelevant answers will be reported

​

Answer 1

They don't need to be pure real or imaginary. Any "mixed" complex number works so long as
`z=z'`.

Let
`z=z'=a+bi`. Then

`|z+z'| = |2a+2bi| = 2 √(a^2+b^2)`

`|z| + |z'| = 2|a+bi| = 2 √(a^2+b^2)`

so
`|z+z'|=|z|+|z'|`.

The geometric interpretation is essentially identical.
`|z+z'|=2|z|` is a complex number twice the distance away from the origin in the complex plane as
`z`, which is exactly
`|z|+|z|`.