Question

What is the smallest natural number in which its digits are only 1's and 2's and which is divisible by 3 and 8?

Answer 1

Look at the multiples of lcm(3, 8) = 24, each of which are divisible by both 3 and 8. Naturally, the number we're looking for must have at least two digits.

The last/ones digit of a number
`n` can be computed by evaluating
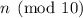`n \pmod{10}`. Suppose the ones digit is 1. Then

`n \equiv 24k \equiv 20k + 4k  \equiv 4k \equiv 1 \pmod{10}`

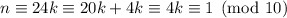
but this has no solution since no multiple of 4 ends in 1. So our number ends with a 2.

If our number has two digits, then in order for it to be divisible by 3, the first digit must be 1, since 1 + 2 = 3. But 12 is not divisible by 24.

If our number has three digits, then it's either 111 (with digital sum 1 + 1 + 1 = 3) or 222 (digital sum 2 + 2 + 2 = 6), since no other triplet of 1s and 2s sums to a multiple of 3. But 111 = 3×37 and 222 = 2×111, so neither are divisible by 24.

Now suppose
`n` has four digits. Also suppose that the tens digit is 2. Then our number must be 1122 to uphold divisibility by 3, but 1122 = 2×3×11×17 is not divisible by 8. So the tens digit must be 1. This in turn leaves two remaining candidates, 1212 and 2112. We have 1212 = 12×(100 + 1) not divisible by 8, so our number must be
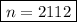`\boxed{n=2112}`. And it is, since 2112 = 24×88.