Question

The length of a rectangle is 6 more than twice the width. if the area is 40 cm^2, find the length and breadth of the rectangle

Answer 1

Answer: 3.217 & 12.434

Explanation:

If we use w to represent the width, the length will be 6 more than 2 times w.

Hence, the length is
`2w+6`.

The area of a rectangle would be its length times its width, so let's make an equation to represent it's area.

`A=w(2w+6)`

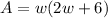
We can also substitute 40 in for A as it's given in the question.

`40 = w(2w+6)`

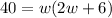
Distributing w by multiplying it by both terms in the parentheses, we get

`40 = 2w^2+6w`

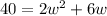
We can make the equation simpler by dividing both sides by 2.

`20 = w^2+3w`

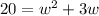
Subtracting both sides by 20 will make the left-hand side 0.

`0=w^2+3w-20`

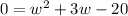
Now that we have put this quadratic equation into standard form (ax²+bx+c), we can find its solutions using the quadratic formula.

For reference, the quadratic formula is

`x=(-b\pm√(b^2-4ac))/(2a)`

In this case, a is 1, b is 3, and c is -20.

Substituting, we get

`w=(-3\pm√(3^2-4(1)(-20)))/(2(1))`

`w= (-3\pm√(9+80))/(2)`

`w=(-3+√(89))/(2)\hspace{0.1cm}or\hspace{0.1cm}(-3-√(89))/(2)`

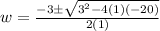
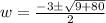
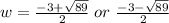
Since the second solution results in a negative number, it cannot be the length of w.

`w=(-3+√(89))/(2)\approx3.217`

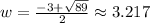
The width/breadth of the rectangle is 3.217 cm.

To calculate the length, let's substitute the width into the expression for the length:

`l=2(3.217)+6`

`l=12.434`

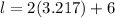
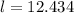
The length of this rectangle is 12.434 cm.