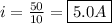Question

A motor has coils with a resistance of 10.0 ohms and is supplied by a voltage of V = 1.20 x 102 V. When the motor is running at its maximum speed, the back emf is 70.0 V. Find the current in the coils (a) when the motor is first turned on and (b) when the motor has reached its maximum rotation rate.

Answer 1

Hi there!

a)
When the motor is first turned on, the coils are initially stationary. Thus, there is no change in magnetic flux and, consequently, no induced emf.

Therefore:

`iR = \epsilon - \epsilon_(back)`

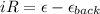
Since there's no back emf:

`iR = \epsilon`

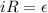
Solving for i using Ohm's Law:

`i = (\epsilon)/(R)\\\\i = (120)/(10) = \boxed{12.0 A}`

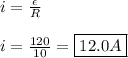
b)

We are given that at max speed, the back EMF is 70.0 V.

Using the same equation as above:

`iR = \epsilon - \epsilon_(back)`

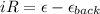
Plugging in the values:

`10i = 120 - 70 \\\\10i = 50 \\\\`

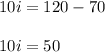
Solving for current:

`i = (50)/(10) = \boxed{ 5.0 A}`