Answer:
0.375 second and 3.5 second
Explanation:
The position can be modeled by a quadratic function
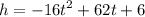 . We are tasked to find the time when a ball reaches a height of 27 feet. Therefore, let h = 27:
. We are tasked to find the time when a ball reaches a height of 27 feet. Therefore, let h = 27:

Solve for t:
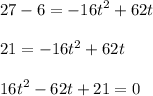
Since the equation is quite complicated and more time-consuming to solve, i'll skip the factoring or quadratic part:
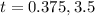
After done solving the equation, you'll get t = 0.375 and 3.5 seconds. These solutions are valid since both are positive values and time can only be positive.
Hence, it'll take 0.375 and 3.5 seconds for a ball to reach 27 feet.