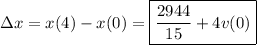1 Answer

Aga · Answer 1 · 2023-03-26T20:42:07+0000

Use the fundamental theorem of calculus.

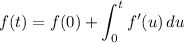
$f(t) = f(0) + \displaystyle \int_0^t f'(u) \, du$

In order to find velocity and position exactly, you need to know the initial velocity and position.

1) Integrate the acceleration function to get the velocity function. By the FTC,

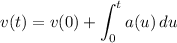
$v(t) = v(0) + \displaystyle \int_0^t a(u) \, du$

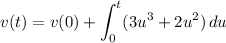
$v(t) = v(0) + \displaystyle \int_0^t (3u^3+2u^2) \, du$

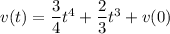
$v(t) = \frac34 t^4 + \frac23 t^3 + v(0)$

At
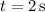$t=2\,\rm s$ , the velocity is

$v(2) = \frac34 2^4 + \frac23 2^3 + v(0) = \boxed{\frac{52}3 + v(0)}$

2) Integrate the velocity function to the get the position function. By the FTC again,

$x(t) = x(0) + \displaystyle \int_0^t v(u) \, du$

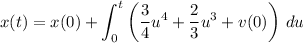
$x(t) = x(0) + \displaystyle \int_0^t \left(\frac34 u^4 + \frac23 u^3 + v(0)\right) \, du$

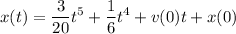
$x(t) = \displaystyle \frac3{20} t^5 + \frac16 t^4 + v(0) t + x(0)$

At
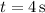$t=4\,\rm s$ , the object's position is

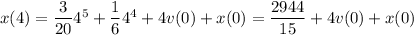
$x(4) = \frac3{20}4^5 + \frac16 4^4 + 4v(0) + x(0) = (2944)/(15) + 4v(0) + x(0)$

Fortunately, you don't need the initial position to find the displacement, since
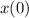x(0) cancels out in the end.

$\Delta x = x(4) - x(0) = \boxed{(2944)/(15) + 4v(0)}$

Please log in or register to add a comment.