Question

Find the area of the following ​

Answer 1

24000 ft²

Explanation:

Triangle PRS:

b = base = PR = 240 ft

2AS = 240 ft

`\sf AS = (240)/(2)\\\\ AS = 120 \ ft`

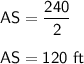
h = height = AS = 120 ft

`\sf \boxed{\bf \ Area \ of \ triangle = (1)/(2)b*h}`

`\sf =(1)/(2)*240*120\\\\ = 120 * 120\\\\ = 14400 \ ft^2`

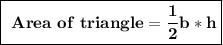
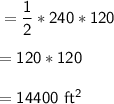
Triangle PRQ:

b = PR = 240 ft

3BQ = 240 ft

`\sf BQ = (240)/(3)\\\\ BQ = 80 \ ft`

`\sf Area \ of \ triangle \ PRQ = (1)/(2)*240*80`

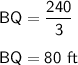
= 120 * 80

= 9600 ft²

Area of the quadrilateral PQRS = area of ΔPRS + area of ΔPRQ

= 14400 + 9600

= 24000 ft²