Question

1)Convert the following binary numbwers into decimal number(only a,b,c,f,i)
​

Answer 1

#1

• (11)_2
• (1×2⁰+1×2¹)_10
• (1(1)+1(2))_10
• (1+2)_10
• (3)_10

#b

• (110)_2
• (0+1×2¹+1×2²)_10
• (2+4)_10
• (6)_10

#c

• (111)_2
• (1×2⁰+1×2¹+1×2²)_10
• (1+2+4)_10
• (7)_10

#f

• (10011)_2
• (1×2⁰+1×2¹+0+0+1×2⁴)_10
• (1+2+16)_10
• (19)_10

#i

• (10110101)_2
• (1×2⁰+0+1×2²+0+1×2⁴+1×2⁵+0+1×2⁷)_10
• (1+4+16+32+128)_10
• (181)_10

Answer 2

a) 3₁₀

b) 6₁₀

c) 7₁₀

f) 19₁₀

i) 181₁₀

Explanation:

Binary to Decimal Conversion (Positional Notation Method)

• Multiply each digit by the base (2) raised to the power dependent upon the position of that digit in the binary number.
• Sum all the values obtained for each digit.
• Express the number as a decimal number by placing subscript 10 after it.

For a binary number with 'n' digits:

• The right-most digit is multiplied by 2⁰
• The left-most digit is multiplied by
  `\sf 2^(n-1)`

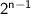
For example, to convert the binary number 111001₂ into a decimal:

`\begin{array}{ c c c c c c}1 & 1 & 1 & 0 & 0 & 1\\\downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow \\2^5 & 2^4 & 2^3 & 2^2 & 2^1 & 2^0\\\end{array}`

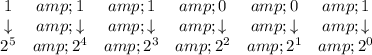
Multiply each digit by the base (2) raised to the power as indicated above and sum them:

`=(1 * 2^5)+(1 * 2^4)+(1 * 2^3)+(0 * 2^2)+(0 * 2^1)+(1 * 2^0)`

`= 32+16+8+0+0+1`

`= 57`

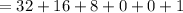
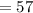
Finally, express as a decimal number ⇒ 111001₂ = 57₁₀

Question (a)

`\begin{aligned}\implies 11_2 & = (1 * 2^1)+(1 * 2^0)\\& = 2+1\\& = 3\end{aligned}`

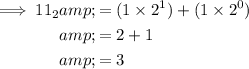
Therefore, 11₂ = 3₁₀

Question (b)

`\begin{aligned}\implies 110_2 & = (1 * 2^2)+(1 * 2^1)+(0 * 2^0)\\& = 4+2+0\\& = 6\end{aligned}`

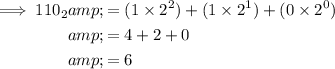
Therefore, 110₂ = 6₁₀

Question (c)

`\begin{aligned}\implies 111_2 & = (1 * 2^2) +(1 * 2^1)+(1 * 2^0)\\& =4+2+1\\& = 7\end{aligned}`

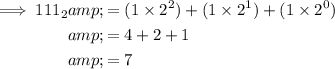
Therefore, 111₂ = 7₁₀

Question (f)

`\begin{aligned}\implies 10011_2 & =(1 * 2^4)+(0 * 2^3)+ (0 * 2^2) +(1 * 2^1)+(1 * 2^0)\\& =16+0+0+2+1\\& = 19\end{aligned}`

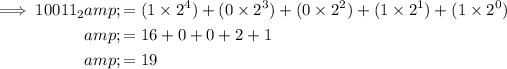
Therefore, 10011₂ = 19₁₀

Question (i)

`\phantom{)))}10110101_2 \\\\=(1 * 2^7)+(0 * 2^6)+(1 * 2^5)+(1 * 2^4)+(0 * 2^3)+ (1 * 2^2) +(0 * 2^1)+(1 * 2^0)\\\\=128+0+32+16+0+4+0+1\\\\= 181`

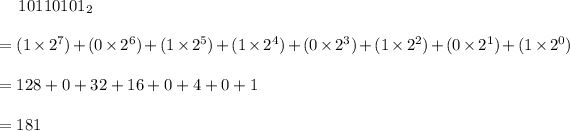
Therefore, 10110101₂ = 181₁₀