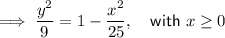Question

MATH HELP!!! 100PTS!!!

Write the parametric equations

x=5sinθ,y=3cosθ,0≤θ≤π

in the given Cartesian form.

(y^2)/9=
with x≥0.

Answer 1

`(y^2)/(9)=1-(x^2)/(25)`

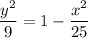
Explanation:

When converting parametric equations that involve trig functions to Cartesian equations, use trig identities to eliminate the parameter.

Given parametric equations:

`x=5 \sin \theta, \quad y=3 \cos \theta, \quad 0\leq \theta\leq \pi`

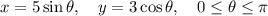
Square the equation for x:

`\implies x^2=(5 \sin \theta)^2=25 \sin^2 \theta`

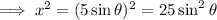
Use the identity
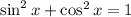`\sin^2 x+\cos^2x =1` to write
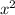`x^2` in terms of cos:

`\implies x^2=25(1-\cos^2 \theta)`

Isolate
`\cos^2 \theta` :

`\implies (x^2)/(25)=1-\cos^2 \theta`

`\implies \cos^2 \theta=1- (x^2)/(25)`

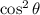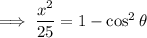
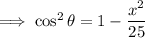
Square the equation for y:

`\implies y^2=(3 \cos \theta)^2=9 \cos ^2 \theta`

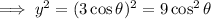
Replace
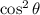`\cos^2 \theta` with the found equation involving
`x^2` :

`\implies y^2=9\left(1-(x^2)/(25)\right)`

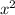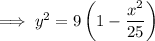
Divide both sides by 9:

`\implies (y^2)/(9)=1-(x^2)/(25), \quad \textsf{with }x\geq 0`