Question

The sequence$$1,2,1,2,2,1,2,2,2,1,2,2,2,2,1,2,2,2,2,2,1,2,\dots$$consists of $1$'s separated by blocks of $2$'s with $n$ $2$'s in the $n^{\rm{th}}$ block. What is the sum of the first $1234$ terms of this sequence

Answer 1

Consider the lengths of consecutive 1-2 blocks.

block 1 - 1, 2 - length 2

block 2 - 1, 2, 2 - length 3

block 3 - 1, 2, 2, 2 - length 4

block 4 - 1, 2, 2, 2, 2 - length 5

and so on.

Recall the formula for the sum of consecutive positive integers,

`\displaystyle \sum_(i=1)^j i = 1 + 2 + 3 + \cdots + j = \frac{j(j+1)}2 \implies \sum_(i=2)^j = \frac{j(j+1) - 2}2`

Now,

`1234 = \frac{j(j+1)-2}2 \implies 2470 = j(j+1) \implies j\approx49.2016`

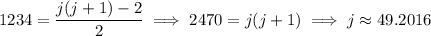
which means that the 1234th term in the sequence occurs somewhere about 1/5 of the way through the 49th 1-2 block.

In the first 48 blocks, the sequence contains 48 copies of 1 and 1 + 2 + 3 + ... + 47 copies of 2, hence they make up a total of

`\displaystyle \sum_(i=1)^48 1 + \sum_(i=1)^(48) i = 48+\frac{48(48+1)}2 = 1224`

numbers, and their sum is

`\displaystyle \sum_(i=1)^(48) 1 + \sum_(i=1)^(48) 2i = 48 + 48(48+1) = 48*50 = 2400`

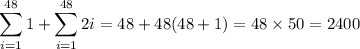
This leaves us with the contribution of the first 10 terms in the 49th block, which consist of one 1 and nine 2s with a sum of
`1+9*2=19`.

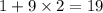So, the sum of the first 1234 terms in the sequence is 2419.