Question

15. The sides of a parallelogram are 100 m each and the length of the longest diagonal is 160 m. Find the area of the parallelogram.​

Answer 1

Area of parallelogram = 9600 m²

Explanation:

• We can find the measure of angle x using the cos rule:

`160^2 = 100^2 +100^2 -2(100)(100) \cdot cos (x)`

Make x the subject of the equation:

⇒
`20000 \cdot cos(x) = 100^2 +100^2 - 160^2`

⇒
`cos(x) = -0.28`

⇒
`x = cos^(-1) (-0.28)`

⇒
`x = 106.26 \textdegree`

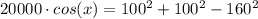
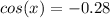
• Now we can find the area of one the triangles formed using the formula:

`Area =(1)/(2) ab \cdot sin \theta`

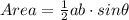
where a and b are two sides of a triangle, and θ is the angle between them (angle x).

Substituting the values:

Area of one triangle =
`(1)/(2)` × (100)(100) × sin(106.26°)

= 4800 m²

• Since the parallelogram is formed by two such triangles, we have to double the area of the triangle to find the parallelogram's area:

Area of parallelogram = 2 × 4800

= 9600 m²