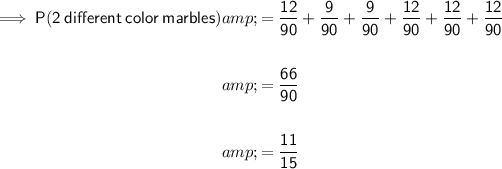Answer:

Explanation:
The bag of marbles contains:
- 3 green marbles
- 3 yellow marbles
- 4 red marbles
⇒ Total marbles = 3 + 3 + 4 = 10
Probability Formula

First draw


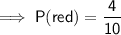
Second draw
As the first marble is not replaced there are now 9 marbles in the bag.
If the first marble was green, the probability of drawing a yellow is now 3/9 and the probability of drawing a red is now 4/9.
If the first marble was yellow, the probability of drawing a green is now 3/9 and the probability of drawing a red is now 4/9.
If the first marble was red, the probability of drawing a green is now 3/9 and the probability of drawing a yellow is now 3/9.
To find the individual probabilities of picking 2 different colors, multiply the probability of the first draw by the probability of the second draw:
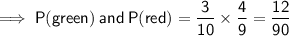

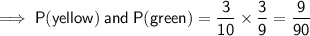
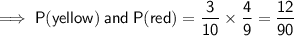
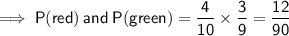

To find the probability of drawing two marbles at random and the marbles being different colors, add the individual probabilities listed above: