Answer:
- a) AB = 10 units
- b) Midpoint is (2, 6)
===================
Given
- Points A( - 1, 10) and B(5, 2)
To find
- a) The length of AB
- b) The midpoint of AB
Solution
a) Use the distance formula:
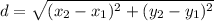
Substitute the coordinates and calculate:
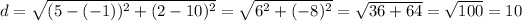
The distance is AB = 10 units
b) Use midpoint formula and find x and y- coordinates of this point:
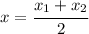 and
and
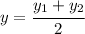
Substitute coordinates and find the midpoint:
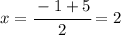 and
and
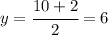
The midpoint is (2, 6)