Question

For the function f(x) = -(x+6)(x+2), when is the function decreasing and when is it increasing?

Answer 1

• The function f is increasing to the left of -4 (-∞ , -4]

• The function f is decreasing to the right of -4 [-4 , +∞)

Explanation:

f(x) = -(x+6)(x+2)

= -(x² + 2x + 6x + 12)

= -(x² + 8x + 12)

= -x² - 8x - 12

The leading coefficient is -1 (the coefficient of the highest term -x² of the trinomial)

Then

The parabola opens downward.

………………………………………

`-(b)/(2a) =-(-8)/(2* \left( -1\right) ) =-4`

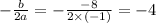
Then

The function f is increasing to the left of -4 (-∞ , -4]

The function f is decreasing to the right of -4 [-4 , +∞)