Question

By what percent does the braking distance of a car decrease, when the speed of the car is reduced by 10.3 percent? Braking distance is the distance a car travels from the point when the brakes are applied to when the car comes to a complete stop.

Answer 1

The braking distance is the distance traveled by a car experiencing a braking force until it comes to rest.

Our initial energy is solely kinetic:

`E_i = (1)/(2)mv^2`

And, since the car goes to rest, it is no longer in motion. It will have no kinetic energy.

`E_f = 0`

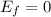
Therefore, there was work done by the braking force.

`W_B = E_f - E_i = -(1)/(2)mv^2`

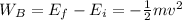
Recall the definition of work:

`W = F\cdot \Delta x`

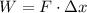
Or in this case, since the displacement and breaking force are antiparallel:

`W = -F_B\Delta x`

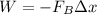
This is equivalent to the dissipation of kinetic energy:

`W = -F_B\Delta x = -(1)/(2)mv^2`

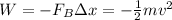
Now, to visualize this, let's rearrange the equation to solve for displacement.

`\Delta x =(mv^2)/(2F_B)`

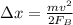
There is a direct, SQUARE relationship between necessary braking distance speed.

If the speed was reduced by 10.3 percent, its new speed is only 89.7% percent of the original, so:

`\Delta x' =(m(0.897v)^2)/(2F_B)`

`\Delta x' = 0.8046\Delta x`

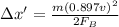
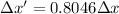
The reduction by a percentage is:

`1 - 0.8046 = 0.1954 \\\\\boxed{= 19.54\%}`