Answer: the total area with the extension S≈82,3 foot², S>S'.
Explanation:
D₁=8 foot D₂=10 foot a wide extension = 4 foot.
1) Let the total area with the extension S is the area of the circular table S₁
plus a wide extension S₂.
Considere S₁:
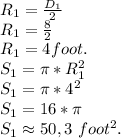
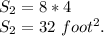
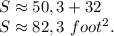
2)\ Considere S':
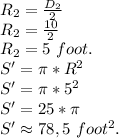
S>S'.
Good luck an' have a nice day!