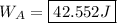Question

A soccer ball is kicked from the top of one building with a height of H1 = 30.2 m to another building with a height of H2 = 12.0 m.

The ball is kicked with a speed of v0 = 15.10 m/s at an angle of θ = 74.1° with respect to the horizontal. The mass of a size 5 soccer ball is m = 450 g. When the ball lands on the other building, its speed is 19.89 m/s.
1. How much energy was lost to air friction? The ball is kicked without a spin.

Answer 1

Hi there!

Initially, we have gravitational potential energy and kinetic energy. If we set the zero-line at H2 (12.0m), then the ball at the second building only has kinetic energy.

We also know there was work done on the ball by air resistance that decreased the ball's total energy.

Let's do a summation using the equations:

`KE = (1)/(2)mv^2 \\\\PE = mgh`

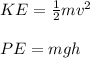
Our initial energy consists of both kinetic and potential energy (relative to the final height of the ball)

`E_i = (1)/(2)mv_i^2 + mg(H_1 - H_2)`

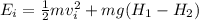
Our final energy, since we set the zero-line to be at H2, is just kinetic energy.

`E_f = (1)/(2)mv_f^2`

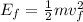
And:

`W_A = E_i - E_f`

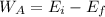
The work done by air resistance is equal to the difference between the initial energy and the final energy of the soccer ball.

Therefore:

`W_A = (1)/(2)mv_i^2 + mg(H_1 - H_2) - (1)/(2)mv_f^2`

Solving for the work done by air resistance:

`W_A = (1)/(2)(.450)(15.1^2)+ (.450)(9.8)(30.2 - 12) - (1)/(2)(.450)(19.89^2)`

`W_A = \boxed{42.552 J}`