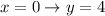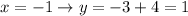Question

Solve the following systems of equations

y= 3x^2 + 6x + 4

Y= -3x^2 + 4

show all work and solutions​

Answer 1

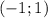`(-1;1)` and
`(0;4)`

Explanation:

First of all, even if the system is of 4th degree, by looking at the shape of the equations I am expecting up to 2 solutions.

The easiest way to solve it, since both equation are in the form y= something, is to equate both RHSs.

`3x^2+6x+4=-3x^2+4\\6x^2+6x=0 \rightarrow 6x(x+1)=0`

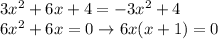
which tells us that either
`x=0` or
`x=-1`

Now we can replace these value of x in one of the two to finish our work:
`x=0\rightarrow y= 4`

`x=-1 \rightarrow y= -3+4=1`