1 Answer

Tom Micheline · Answer 1 · 2023-01-06T14:45:16+0000

Compute the gradient of
.

$\\abla f(x,y) = \left\langle 3x^2 - 6y, -6x + 3y^2\right\rangle$

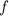Set this equal to the zero vector and solve for the critical points.

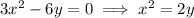
$3x^2-6y = 0 \implies x^2 = 2y$

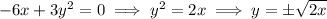
$-6x+3y^2=0 \implies y^2 = 2x \implies y = \pm√(2x)$

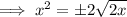
$\implies x^2 = \pm2√(2x)$

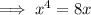
$\implies x^4 = 8x$

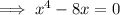
$\implies x^4 - 8x = 0$

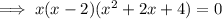
$\implies x (x-2) (x^2 + 2x + 4) = 0$

$\implies x = 0 \text{ or } x-2 = 0 \text{ or } x^2 + 2x + 4 = 0$

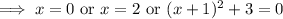
$\implies x = 0 \text{ or } x = 2 \text{ or } (x+1)^2 + 3 = 0$

The last case has no real solution, so we can ignore it.

Now,

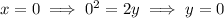
$x=0 \implies 0^2 = 2y \implies y=0$

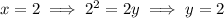
$x=2 \implies 2^2 = 2y \implies y=2$

so we have two critical points (0, 0) and (2, 2).

Compute the Hessian matrix (i.e. Jacobian of the gradient).

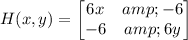
$H(x,y) = \begin{bmatrix} 6x & -6 \\ -6 & 6y \end{bmatrix}$

Check the sign of the determinant of the Hessian at each of the critical points.

$\det H(0,0) = \begin{vmatrix} 0 & -6 \\ -6 & 0 \end{vmatrix} = -36 < 0$

which indicates a saddle point at (0, 0);

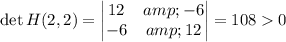
$\det H(2,2) = \begin{vmatrix} 12 & -6 \\ -6 & 12 \end{vmatrix} = 108 > 0$

We also have
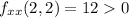f_(xx)(2,2) = 12 > 0 , which together indicate a local minimum at (2, 2).

Please log in or register to add a comment.