Question

A uniform rod with a mass of m = 1.94 kg and a length of l = 2.10 m is attached to a horizontal surface with a hin ge. The rod can rotate around the hin ge without friction.

Initially the rod is held at rest at an angle of θ = 70.4° with respect to the horizontal surface. Then the rod is released.
1. What is the angular speed of the rod, when it lands on the horizontal surface?
2. What is the angular acceleration of the rod, just before it touches the horizontal surface?

Answer 1

Hello!

1.

To solve, we can use the work-energy theorem.

Initially, the rod is at rest. Its center of mass is some height above the surface, so it contains gravitational potential energy.

Finally, the rod has rotational kinetic energy.

To find the initial energy, we have to find where the center of mass is. It is located at the midpoint of the rod, or l/2. To find its height above, though, we have to find its sine component with respect to the angle:

`E_i = mg{(l)/(2)}}sin(\theta)`

Its final energy:

`E_f = (1)/(2)I\omega^2`

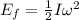
About the pivot point, a rod's moment of inertia (I) is 1/3ml².

`E_f = (1)/(2)((1)/(3)ml^2) = (1)/(6)ml^2\omega^2`

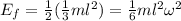
Now, solving for angular speed:

`E_i = E_f\\\\mg(l)/(2)sin\theta = (1)/(6)ml^2 \omega^2\\\\3gsin\theta = l\omega^2 \\\\\omega = \sqrt{(3gsin\theta)/(l)}`

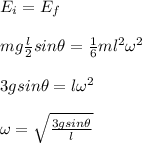
Plugging in the values and solving:

`\omega = \sqrt{(3(9.8)sin(70.4))/(2.1)} = \boxed{3.63 rad/s}`

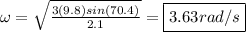
2.

Let's determine where to place our pivot point. To minimize the number of torques to take into account, let's put the pivot point at the base of the rod.

Now, the only torque we must consider is that produced by the force of gravity.

Recall the equation for torque:

`\tau = r * F`

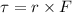
This is a cross-product, where 'r' is the lever arm of the force. This is the perpendicular distance between the line of action of the force and the pivot point.

In this instance, based on our reference angle, this would be the COSINE.

`\tau = rFcos\theta`

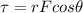
r = distance from pivot point to center of the rod (1.05 m)

F = Force of gravity, mg (19.03 N)

θ = angle of rod from horizontal

Using the rotational equivalent of Newton's Second Law:

`I\alpha = rFcos\theta`

'I' is the rod's moment of inertia about the pivot point. For a uniform rod, its moment of inertia at its end is 1/3ml².

Therefore:

`I = (1)/(3)(1.94)(2.1^2) = 2.85 kgm^2`

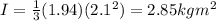
Now, we can solve for the function for angular acceleration.

`\alpha(\theta) = (rF)/(I)cos\theta\\\\\alpha(\theta) = ((1.05)(19.03))/(2.85)cos\theta = 7cos\theta`

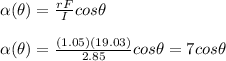
This is the angular acceleration of the rod as a function of theta.

Substituting in θ = 0°:

`\alpha(0) = 7cos(0) = \boxed{7 rad/s^2}`

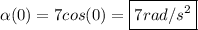
**Note, we couldn't just use rotational kinematics because the angular acceleration is NOT constant.