Question

100 POINTS!!! Find the exact length of side a.
Has to be one of the four options

Answer 1

Answer: a = 2√3

First method (Pythagoras theorem):

a² + b² = c²

a² + 2² = 4²

a² = 16 - 4

a = √12

a = 2√3

Second method (sine rule):

opposite/hypotenuse = sin(x)

a/4 = sin(60)

a = 4sin(60)

a = 2√3

Third method (tan rule):

opposite/adjacent = tan(x)

a/2 = tan(60)

a = 2tan(60)

a = 2√3

Answer 2

2√3

Explanation:

From inspection of the given triangle:

• Side a is opposite angle A ⇒ a = BC
• Side b is opposite angle B ⇒ b = AC
• Side c is opposite angle C ⇒ c = AB

As we cannot be sure that ΔABC is a right triangle since it is not marked as such, use the cosine rule to find the exact length of side a.

Cosine Rule

`a^2=b^2+c^2-2bc \cos A`

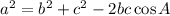
where a, b and c are the sides and A is the angle opposite side a

Given:

• A = 60°
• b = 2
• c = 4

Substitute the given values into the formula and solve for a:

`\implies a^2=2^2+4^2-2(2)(4) \cos 60^(\circ)`

`\implies a^2=4+16-16\left((1)/(2)\right)`

`\implies a^2=20-8`

`\implies a^2=12`

`\implies a=√(12)`

`\implies a=√(4 \cdot 3)`

`\implies a=√(4){√(3)`

`\implies a=2√(3)`

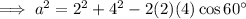
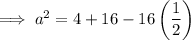
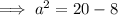
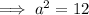
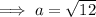
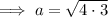
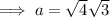
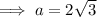
Therefore, the exact length of side a is 2√3.

To find out if ΔABC is a right triangle, use Pythagoras Theorem to solve for side a:

`\implies a^2+b^2=c^2`

`\implies a^2+2^2=4^2`

`\implies a^2+4=16`

`\implies a^2=12`

`\implies a=√(12)`

`\implies a=2√(3)`

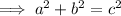
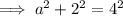
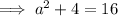
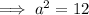
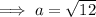
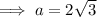
As the measure of side a is the same as the solution found when using the cosine rule, we can conclude that ΔABC is a right triangle.