Question

A stone of mass 150g is rotated in a horizontal circle at 10m/s which is attached to the end of a 1m long. what will be the acceleration of the stone and it's centripetal force?​

Answer 1

force is mass multiply by acceleration so it will be 150 multiply by 10 is 1500N

Answer 2

Acceleration:
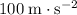`100\; {\rm m\cdot s^(-2)}` assuming that the radius of the rotation is
`1\; {\rm m}`.

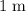Centripetal force:
`15\; {\rm N}`.

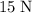Step-by-step explanation:

In a circular motion, if the tangential velocity is
`v` and the radius of the motion is
`r`, the centripetal acceleration of the motion would be
`a = (v^(2) / r)`.

In this question, it is implied that for this circular motion,
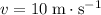`v = 10\; {\rm m\cdot s^(-1)}` while
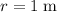`r = 1\; {\rm m}`. Thus, the (centripetal) acceleration would be:

`\begin{aligned} a &= (v^(2))/(r) \\ &= \frac{(10\; {\rm m\cdot s^(-2)})^(2)}{1\; {\rm m}} \\ &= 100\; {\rm m \cdot s^(-2)}\end{aligned}`.

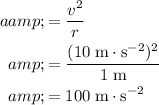Note that the unit of mass in this question is gram, whereas the standard unit for mass should be
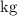`{\rm kg}` (so as to leverage the fact that
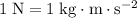`1\; {\rm N} = 1\; {\rm kg \cdot m \cdot s^(-2)}`.) Apply unit conversion:
`m = 150\; {\rm g} = 0.150\; {\rm kg}`.

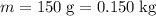Using that fact that
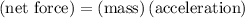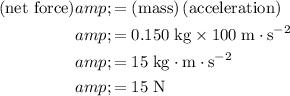`(\text{net force}) = (\text{mass}) \, (\text{acceleration})`:

`\begin{aligned} (\text{net force}) &= (\text{mass}) \, (\text{acceleration}) \\ &= 0.150\; {\rm kg} * 100\; {\rm m\cdot s^(-2)} \\ &= 15\; {\rm kg \cdot m \cdot s^(-2)} \\ &= 15\; {\rm N}\end{aligned}`.