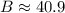Question

Use the Law of Cosines to find the specified missing value. Approximate your answer to the nearest tenth.

If A = 60°, b = 20 ft, c = 30 ft, find B.

Answer 1

40.9

Explanation:

Law Of Cosines:

`cos(A)=(b^2+c^2-a^2)/(2bc)`

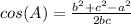
This can generally be understand as the cosine(angle) = the sum of squares of the two other sides - the opposite side squares divided by 2 times the other two sides

If this is to confusing to understand I'll just provide the formula for the other two angles which is essentially the same thing just different variables

`cos(B)=(a^2+c^2-b^2)/(2ac)\\\\cos(C)=(a^2+b^2-c^2)/(2ab)`

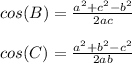
Anyways for the law of cosines we need all three sides, but since we're given the two other sides, we can also rearrange the equation to solve for the other missing side.

Original Equation

`cos(A)=(b^2+c^2-a^2)/(2bc)\\`

Multiply both sides by 2bc

`cos(A)*2bc=b^2+c^2-a^2`

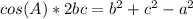
Add a^2 to both sides

`cos(A)*2bc+a^2=b^2+c^2`

Subtract 2bc * cosA from both sides

`a^2=b^2+c^2-2bc*cos(A)`

So this can be applied for any side, and it can be generally seen as: side ^2 = sum of squares of other two sides - 2 times the other two sides * cos(opposite angle of the original side). If that's to confusing you can also just look at the other formulas which are essentially the same just different variables

`b^2=a^2+c^2-2ac * cos(B)\\c^2=a^2+b^2-2ab*cos(C)`

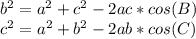
anyways, applying this formula we get the equation:

`a^2=20^2+30^2-2(20)(30)*cos(60)`

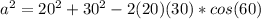
Square and multiply values you get

`a^2=400+900-1200*cos(60)`

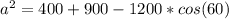
Now add the values and you can calculator cos(60) using a calculator or using the unit circle, both should give the same value

`a^2=1300-1200(0.5)`

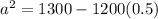
Multiply

`a^2=1300-600`

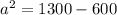
Simplify

`a^2=700`

Take the square root of both sides

`a\approx 26.4575`

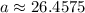
So now use this to solve for B using the original law of cosines equation. Plugging in all the sides you get the equation:

`cos(B)=(26.4575^2+30^2-20^2)/(2(26.4575)(30))`

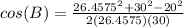
Square values and simplify denominator

`cos(B)=(700+900-400)/(1,587.451)`

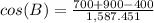
Simplify numerator

`cos(B)=(1200)/(1,587.451)`

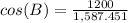
Convert to decimal

`cos(B)\approx 0.755`

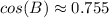
Take the inverse cosine of both sides

`B \approx cos^(-1)(0.755)`

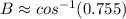
Approximate this using a calculator

`B\approx 40.8934`

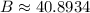
Round to the nearest tenth

`B\approx40.9`