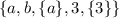Question

What is the number of Power set of A show step by step? A = {a,b, {a}, 3, {3}}.​

Answer 1

By "number of Power set of A" I wonder if you mean the cardinality of the power set.

For any finite set with
`n` elements, its power set contains
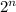`2^n` elements.

Here
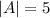`|A| = 5`, so the power set will contain
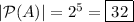`|\mathcal P(A)| = 2^5 = \boxed{32}` elements.

Recall that the power set is the set of all subsets of a given set

• subsets of
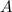`A` of size 0 (1):

`\emptyset`

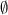
• subsets of size 1 (5):

`\{a\}\\ \{b\}\\ \{\{a\}\}\\ \{3\}\\ \{\{3\}\}`

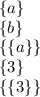
• subsets of size 2 (10):

`\{a,b\}\\ \{a,\{a\}\}\\ \{a, 3\}\\ \{a, \{3\}\}\\ \{b,\{a\}\}\\ \{b,3\}\\ \{b,\{3\}\}\\ \{\{a\},3\}\\ \{\{a\}, \{3\}\}\\ \{3,\{3\}\}`

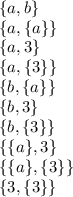
• subsets of size 3 (10):

`\{a,b,\{a\}\}\\ \{a,b,3\}\\ \{a,b,\{3\}\}\\ \{a,\{a\},3\}\\ \{a,\{a\},\{3\}\} \\ \{a,3,\{3\}\}\\ \{b,\{a\},3\}\\ \{b,\{a\},\{3\}\}\\ \{\{a\},3,\{3\}\}`

• subsets of size 4 (5):

`\{a,b,\{a\},3\}\\ \{a,b\{a\},\{3\}\}\\ \{a,b,3,\{3\}\}\\ \{a,\{a\},3,\{3\}\}\\ \{b,\{a\},3,\{3\}\}`

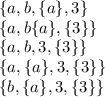
• subsets of size 5 (1):

`\{a,b,\{a\},3,\{3\}\}`