Question

Set up an algebraic equation and then solve.

The width of a rectangle is 14 units less than the length. If the area is 120 square
units, then find the dimensions of the rectangle.
Length:
Width:

Answer 1

Width: 6

Length: 20

Explanation:

So the area of a rectangle can be defined as:
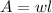`A=wl` where w=width and l=length.

In this case we don't know what the length is, so let's just say the length is the variable l, and since the width is 14 units less than the length, we can express it as (l-14). this gives us the equation:
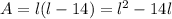`A=l(l-14)=l^2-14l`. We can solve for l, since we're given the area which is 120. So let's set the equation equal to that:

Original Equation:

`A=l^2-14l`

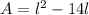
Substitute 120 as A (given)

`120=l^2-14l`

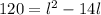
There is many ways to solve this equation: factoring, quadratic equation, completing the square etc... but in this case I'll just complete the square

Add (b/2)^2 to both sides to complete the square

`120+((-14)/(2))^2=l^2-14l+((-14)/(2))^2`

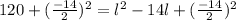
Simplify

`169=l^2-14l+49`

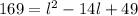
Rewrite right side a square binomial

`169=(l-7)^2`

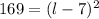
Take the square root of both sides

`13=l-7\\`

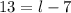
Add 7 to both sides

`20=l`

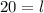
to solve for width simply subtract 14 from the length which is 20, so the width is 6

Width: 6

L: 20