Question

the Royal fruit company produces two types of fruit drinks the first type is 45% pure fruit juice and the second type is 95% pure fruit juice. the company is attempting to produce a fruit drink that contains 55% pure fruit juice how many pints of each of the two existing types of drink must be used to make 180 pints of a mixture that is 55% pure fruit juice ​

Answer 1

first type: 144 pints

second type: 36 pints

Explanation:

So let's try to interpret the given information. So the first thing to know is how to calculate x%, to calculate this, you simply multiply the number by x/100, which is what x is in decimal form.

So let's just start off by assigning variables to each brand, with the variable representing the amount of pints. Let's say "x" is the amount of pints of the first brand, and "y" is the amount of pints of the second brand.

The next thing to do is make equations using the given information. So we want a fruit drink that is 55% pure fruit juice, and it's 180 pints. So to find what 55% is, we multiply by 55/100 or 0.55. This means that 55% is 0.55(180) = 99. So using the given information this means that 99 pints is pure fruit juice in the mixture. This comes from mixing the first two brands, so that means if we take the pure fruit juice from the first brand and add it to the second brand we get 99, and remember we are given the information that 45% of the first brand is pure fruit juice and the second is 95%, this means that 0.45x is pure fruit juice in the first brand and 0.95y is pure fruit juice in the second brand. This sets up the following equation:
`99 = 0.45x + 0.95y`

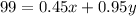
The second equation to set up is using the total amount of pints. x represents how much is from the first brand, and y represents how much is from the second brand. Since the mixture consists of these two brands, and the mixture is 180 pints we can form the equation:
`180 = x+y`

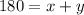
The last step is to solve the systems of equations using the two equations we formed. This can be done via substitution. We simply need to solve for either x or y, in the total amount of pints equation and then substitute it into the pure fruit juice equation. In this example I'll solve for x

Original Equation:

`180 = x+y`

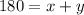
Subtract y from both sides

`180-y=x`

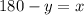
So now that we solved for y in terms of x we can substitute this into the pure fruit juice equation, so that we're only dealing with one variable.

Original Equation:

`99 = 0.45x + 0.95y`

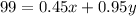
Substitute 180-y as x

`99 = 0.45(180-y) + 0.95y`

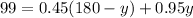
Distribute the 0.45

`99=81-0.45y+0.95y`

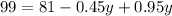
Add like terms

`99=81+0.5y`

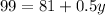
subtract 81 from both sides

`18=0.5y`

Divide both sides by 0.5 (same thing as multiply by 2)

`36=y`

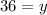
This means we have to use 36 pints of the second brand. We can substitute this into either equation to solve for x, but it's easier to substitute into the total pints equation since there are no coefficients (technically a 1 in front, but it's kind of be ignored for now), so it's pretty straightforward to solve for x

Original Equation:

`180=x+y`

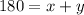
Substitute 36 as y

`180=x+36`

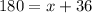
Subtract 36 from both sides

`144=x`

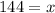
This means 144 pints from the first brand and 36 from the second