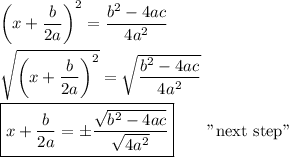Question

The steps to derive the quadratic formula are shown below:

I need help pls

Step 1 ax2 + bx + c = 0
Step 2 ax2 + bx = − c
Step 3 x2 + b over a times x equals negative c over a
Step 4 x2 + b over a times x plus b squared over 4 times a squared equals negative c over a plus b squared over 4 times a squared
Step 5 x2 + b over a times x plus b squared over 4 times a squared equals negative 4 multiplied by a multiplied by c, all over 4 multiplied by a squared plus b squared over 4 times a squared
Step 6


Provide the next step to derive the quadratic formula. (1 point)

x plus b over 2 times a equals plus or minus b squared minus 4 times a times c all over the square root of 4 times a squared

x plus b over 2 times a equals plus or minus b minus 2 times a times c all over square root of 2 times a

x plus b over 2 times a equals plus or minus the square root of the quantity b squared minus 4 times a times c all over the square root of 4 times a squared

x plus b over 2 times a equals plus or minus the square root of the quantity b squared minus 4 times a times c all over the square root of 2 times a

Answer 1

Answer:
`x+(b)/(2a)=\pm (√(b^2 - 4ac))/(√(4a^2))`

Explanation:

We can rewrite the left hand side as a perfect square, more specifically

`\left(x+(b)/(2a) \right)^2`

So, taking the square root of both sides,

`x+(b)/(2a)=\pm (√(b^2 - 4ac))/(√(4a^2))`

Answer 2

(c) x plus b over 2 times a equals plus or minus the square root of the quantity b squared minus 4 times a times c all over the square root of 4 times a squared

Explanation:

The next step is to take the square root of both sides of the equation. It can help to show the intermediate steps.

Result so far

The last step shown in the derivation so far is ...

`x^2+(b)/(a)x+(b^2)/(4a^2)=-(4ac)/(4a^2)+(b^2)/(4a^2)`

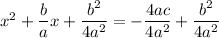
Next step

The left side of the above expression can be written as a square, and the right side can be written over one denominator. Then the square root is taken as the next step.

`\left(x+(b)/(2a)\right)^2=(b^2-4ac)/(4a^2)\\\\\sqrt{\left(x+(b)/(2a)\right)^2}=\sqrt{(b^2-4ac)/(4a^2)}\\\\\boxed{x+(b)/(2a)=\pm(√(b^2-4ac))/(√(4a^2))}\qquad\text{`