Answer:

Explanation:
The gist of modular arithmetic in a nutshell: the numbers
 and
and
 are considered to be congruent by their modulus
are considered to be congruent by their modulus
 if
if
 is a divisor of their difference.
is a divisor of their difference.
In mathematics:
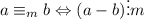
Exemplifying this:
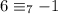 because
because
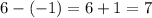 ,
,
 .
.
Let us have following equivalences:
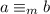 and
and
 , then:
, then:
 and
and
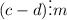 by definition.
by definition.
Properties:
1.
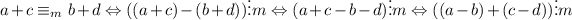 .
.
2.
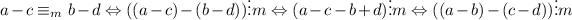 .
.
3.
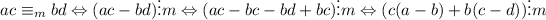 .
.
4. What if we have
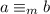 twice? If we abide by property 3, we can come to the conclusion that
twice? If we abide by property 3, we can come to the conclusion that
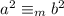 . It is fair enough that there is room for the equivalence
. It is fair enough that there is room for the equivalence
 .
.

Notice that
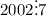 already. There is no need to consider the rest multipliers because the product is
already. There is no need to consider the rest multipliers because the product is
 anyways, we can cut corners in this regard.
anyways, we can cut corners in this regard.
We used property 4.
Recapitulating this: our remainder is
 .
.