Answer:
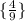
Explanation:
First off, we are given a parabola by definition:
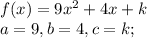
Since
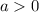 , our parabola has an upward opening.
, our parabola has an upward opening.
Should we think about it graphically, it will be no wonder that we should pay our attention to the points of the parabola intersecting the abscissa axis. In other words, we need our vertex to intersect the x axis only once per se.
The vertex:
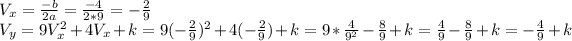
As a result, our
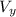 is parametric.
is parametric.
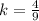 suits us because
suits us because
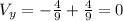 . If
. If
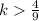 , we do not have any roots at all. We have two roots if
, we do not have any roots at all. We have two roots if
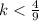 .
.