Question

Need help with this question. ​

Answer 1

We have this equation:

`\log(x) + \log(x + 99) = 2`

First, combine both logarithms using the multiplication property and simplify the expression.

`\log[x(x + 99)] = 2`

`\log[ {x}^(2) + 99x ] = 2`

Now, use the definition of logarithm to transform the equation.

`{10}^(2) = {x}^(2) + 99x`

`{x}^(2) + 99x - 100 = 0`

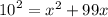
Finally, use the quadratic formula to solve the equation.

`x = \frac{ -99 ± \sqrt{ {99}^(2) - 4 * 1 * ( - 100)} }{2 * 1}`

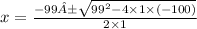
With this, we can say that the solution set is:

• x = 1
• x = -100

We cannot choose x = -100 as a solution because we cannot have a negative logarithm. The only solution is x = 1.