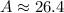Answer:
26.4
Explanation:
Law Of Cosines:
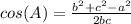
This should work for any side. This can generally be thought as:
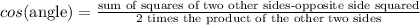
If this is too confusing here's the formula for the other sides (which is essentially the same, just different variables)
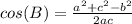
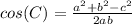
Anyways now just plug in the known values into the equation
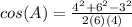
Square and multiply values
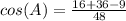
Add the values in the numerator
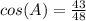
Take the inverse of cosine on both sides
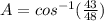
calculate arccosine (inverse cosine) using a calculator
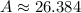
Round to nearest tenth