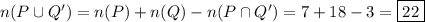By inclusion/exclusion,
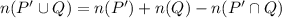
We have

so that
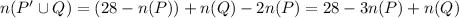
Now,
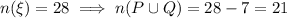
and by inclusion/exclusion,
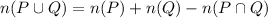
Decompose
 into the union of two disjoint sets:
into the union of two disjoint sets:
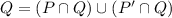
Since they're disjoint,
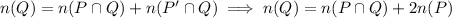
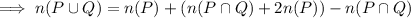
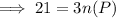
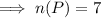
From the Venn diagram, we see there are 3 elements unique to
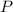 - by the way, this is the set
- by the way, this is the set
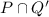 - so
- so
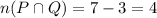 , and it follows that
, and it follows that
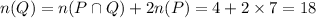
Finally, we get for (a)
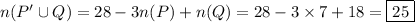
For (b), we have by inclusion/exclusion that