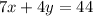Question

Please help!

Using the graph below, which of the following equations represents the line that is parallel to line FG and passes through the (8,−3) point?


my only answers can be the ones in the attached image (just had a random one ticked)

Answer 1

the second option:
`7x+4y=44`

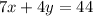
Explanation:

So when a line is parallel, it means that it has the same slope and a different y-intercept, it's important that there is a different y-intercept, otherwise it would be the same line, and the "two lines" would intersect at infinite points.

Anyways by looking at the graph you have two points (-8, 5) and (-4, -2). So the run in this case was 4 and the rise was -7. This is a slope of -7/4. So we have the equation:
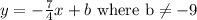`y=-(7)/(4)x+b \text{ where b}\\e-9}`. Since it passes through the point (8, -3) we can plug that in as (x, y) to solve for b (the y-intercept)

Plug in (8, -3) as (x, y)

`-3=-(7)/(4)(8)+b`

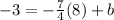
Multiply the -7/4 and 8

`-3 = -14+b`

add 4 to both sides

`11 = b`

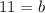
So this gives us the equation:

`y=-(7)/(4)x+11`

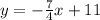
Since it's asking for it in standard form you move the 7/4 x to the other side

Add 7/4x to both sides

`(7)/(4)x+y=11`

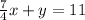
Multiply both sides by 4 to cancel out the fraction

`7x+4y=44`