Answer:
3
Step-by-step explanation:
A solution to a function is when the graph of the function crosses the x-axis. In other words, it's a point where y = 0. So, we can set x^3 + kx^2 - 9x -18 equal to 0. Note that there is an unknown coefficient in this equation (k) that we have to solve for. We are given that one solution to this equation is -2. This means that we can plus x = -2 into the equation and solve for the unknown k:
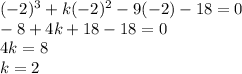
Therefore, the complete equation is the following:
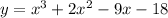
As it turns out, we can use grouping to factor this polynomial. Let's start by re-ordering the terms to visualize it better:
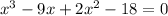
The first two terms have a GCF of x, and the last two terms have a GCF of 2:
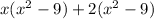
Now, there is a common term that we can bring to the front to complete our factoring process:
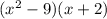
First of all, note that x+2 is one of the factors, and if this was set to 0, we would get -2, which is consistent with the problem. Also, note that our other term can be factored more because it is a difference of two squares:
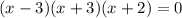
If we set each term to 0, we get x = 3, x = -3, and x = -2. We are only looking for the positive solution to this equation, which is 3