Question

X^3(x^2-13)=-36x
If x>0, what is one possible solution to the equation shown above?

Answer 1

`\{2\} \cup \{3\}`

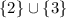
Step-by-step explanation:

`x^3(x^2 - 13) = -36x; \\ x^3(x^2 - 13) + 36x = 0; \\ x(x^2(x^2 - 13) + 36)=0; \\ x(x^4 - 13x^2 + 36) = 0 \\ \left \ [ {{x = 0} \atop {x^4 - 13x^2 + 36 = 0}} \right.`

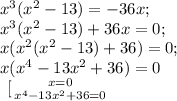
We have two equalities.

Let us analyze the latter.

Let
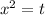`x^2 = t` on condition that
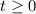`t \geq 0`, then:

`t^2 - 13t + 36 = 0; \\ a = 1, b = -13, c = 36; \\ D = b^2 - 4ac = (-13)^2 - 4 * 1 * 36 = 169 - 144 = 25 = 5^2, > 0; \\ t_(1, 2) = (-b \pm √(D))/(2a) = (-(-13) \pm √(5^2))/(2 * 1) = (13 \pm 5)/(2) = \ [ {{(13 - 5)/(2) = (8)/(2) = 4 } \atop {(13 + 5)/(2) = (18)/(2) = 9 }} \right.`

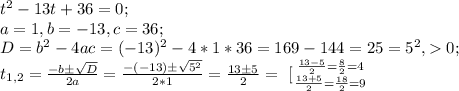
Substitute
`t` back for
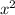`x^2`, keep in mind that
`t \geq 0`.

`\left \ [ {{x^2 = 4} \atop {x^2 = 9}} \right. \Leftrightarrow \left \ [ {{x = \pm 2} \atop {x = \pm 3}} \right.`

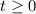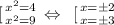
Therefore,
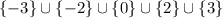`\{-3\} \cup \{-2\} \cup \{0\} \cup \{2\} \cup \{3\}` is our set of solutions. Given the condition that we need our variable to be more than zero, our answer is
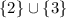`\{2\} \cup \{3\}`.