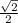Answer:
{
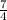 -
-
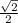 ,
,
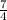 +
+
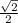 }
}
Explanation:
ax² + bx + c = 0
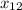 = ( - b ±
= ( - b ±
 ) ÷ 2a
) ÷ 2a
~~~~~~~~~~~
g(x) = 3x - 7
g²(x) = (3x - 7)²
g²(x) = 9x² - 42x + 49
g²(
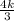 ) = 9(
) = 9(
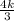 )² - 42(
)² - 42(
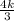 ) + 49
) + 49
9(
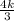 )² - 42(
)² - 42(
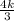 ) + 49 = 8
) + 49 = 8
16k² - 56k + 41 = 0
a = 16 , b = - 56 , c = 41
D = b² - 4ac = ( - 56)² - 4(16)(41) = 512 =
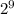
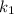 = ( 56 + √
= ( 56 + √
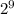 ) ÷ 32 =
) ÷ 32 =
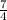 +
+
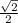
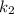 =
=
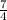 -
-