Answer:
28.31
Explanation:
So in this case you're going to need to use the law of sines which essentially states that:
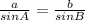 which should apply to any of the sides. the lowercase a and b are the opposite sides of the angles A and B. In this example the angle A is given and C is given, but not in the text. Since you have the right angle thing in the diagram, angle C is a right angle (90 degrees).
which should apply to any of the sides. the lowercase a and b are the opposite sides of the angles A and B. In this example the angle A is given and C is given, but not in the text. Since you have the right angle thing in the diagram, angle C is a right angle (90 degrees).
Given information:
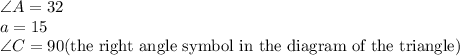
Law of sines equation:

Plug in known information:

since sin(90) = 1, simplify the fraction

Calculate sin(32)
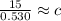
Divide
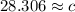
If you haven't learned law of sines yet and don't quite understand why it works you can also use the definition of tan to find what b equals and then use the Pythagorean Theorem to solve for c
tan is defined as:
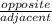
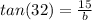
now multiply both sides by b
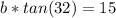
Divide both sides by tan 32

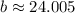
Now use the Pythagorean Theorem:

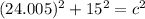
Square known values
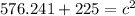
Add the values
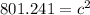
take the square root of both sides
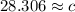
Rounding to the nearest hundredth gives you 28.31