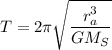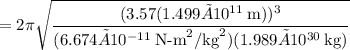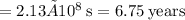Step-by-step explanation:
Given:

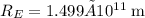
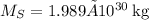
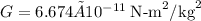
Let
 = mass of the asteroid and
= mass of the asteroid and
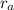 = orbital radius of the asteroid around the sun. The centripetal force
= orbital radius of the asteroid around the sun. The centripetal force
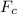 is equal to the gravitational force
is equal to the gravitational force
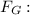
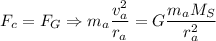
or
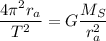
where
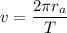
with T = period of orbit. Rearranging the variables, we get
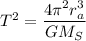
Taking the square root,