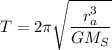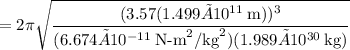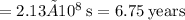Question

An asteroid is discovered in a nearly circular orbit around the Sun, with an orbital radius that is 3.570 times Earth's. What is the

asteroid's orbital period, in terms of Earth years?
orbital period:
years

Answer 1

Step-by-step explanation:

Given:

`r_a = 3.570R_E`

`R_E = 1.499×10^(11)\:\text{m}`

`M_S = 1.989×10^(30)\:\text{kg}`

`G = 6.674×10^(-11)\:\text{N-m}^2\text{/kg}^2`

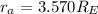
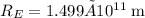
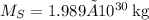
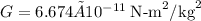
Let
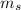`m_s`= mass of the asteroid and
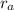`r_a` = orbital radius of the asteroid around the sun. The centripetal force
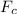`F_c` is equal to the gravitational force
`F_G:`

`F_c = F_G \Rightarrow m_a(v_a^2)/(r_a) = G(m_aM_S)/(r_a^2)`

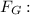
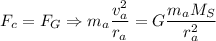
or

`(4\pi^2 r_a)/(T^2) = G(M_S)/(r_a^2)`

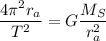
where

`v = (2\pi r_a)/(T)`

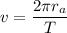
with T = period of orbit. Rearranging the variables, we get

`T^2 = (4\pi^2 r_a^3)/(GM_S)`

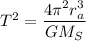
Taking the square root,

`T = 2\pi \sqrt{(r_a^3)/(GM_S)}`

`\:\:\:\:=2\pi \sqrt{\frac{(3.57(1.499×10^(11)\:\text{m}))^3}{(6.674×10^(-11)\:\text{N-m}^2\text{/kg}^2)(1.989×10^(30)\:\text{kg})}}`

`\:\:\:\:= 2.13×10^8\:\text{s} = 6.75\:\text{years}`