Question

Consider 4.00 L of a gas at 365 mmHg and 20. ∘C . If the container is compressed to 2.80 L and the temperature is increased to 30. ∘C , what is the new pressure, P2 , inside the container? Assume no change in the amount of gas inside the cylinder.

Answer 1

This is an exercise in the General Combined Gas Law.

To start solving this exercise, we obtain the following data:

Data:

• V₁ = 4.00 l
• P₁ = 365 mmHg
• T₁ = 20 °C + 273 = 293 K
• V₂ = 2,80 l
• T₂ = 30 °C + 273 = 303 K
• P₂ = ¿?

We apply the following formula:

• P₁V₁T₂=P₂V₂T₁ ⇒ General formula

Where:

• P₁=Initial pressure
• V₁=Initial volume
• T₂=end temperature
• P₂=end pressure
• T₂=end temperature
• V₁=Initial temperature

We clear for final pressure (P2)

`\large\displaystyle\text{$\begin{gathered}\sf P_(2)=(P_(1)V_(1)T_(2))/(V_(2)T_(1)) \ \ \to \ \ \ Formula \end{gathered}$}`

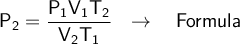
We substitute our data into the formula:

`\large\displaystyle\text{$\begin{gathered}\sf P_(2)=\frac{(365 \ mmHg)(4.00 \\ot{l})(303 \\ot{K})}{(2.80 \\ot{l})(293\\ot{K})} \end{gathered}$}`

`\large\displaystyle\text{$\begin{gathered}\sf P_(2)=(442380 \ mmHg)/( 820.4 ) \end{gathered}$}`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf P_(2)=539.224 \ mmHg \end{gathered}$}}`

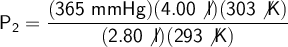
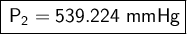
Answer: The new canister pressure is 539.224 mmHg.

{ Pisces04 }