Answer:
y = (-3/2)x
Explanation:
I am going to answer this question in slope-intercept form, which is y = mx + b (m is the slope, b is the y-intercept). The question already gives us the y-intercept, or the point at which the graph crosses the y-axis. It is (0, 0). Now, all we have to do is find the slope, which we can do using the following formula:
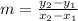
In this formula, (x1, y1) and (x2, y2) are two points that are given to us [the first point is (0,0) and the second point is (2,-3). We can solve for the slope by plugging in:
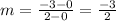
Now that we have m and b, we can plug into slope-intercept form to get our equation: y = (-3/2)x + 0 or y = (-3/2)x