Answer:
Proof below
Explanation:
General outline
- Lemma regarding remainders of non-small primes divided by 6
- Check
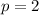 and
and
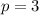 directly
directly - Proof the rest by contradiction
Lemma
If
 is prime such that
is prime such that
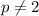 and
and
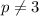 , then
, then
 divided by 6 has remainder of 1 or 5.
divided by 6 has remainder of 1 or 5.
Case 1: p/6 has remainder 0, 2, or 4.
Then there exists some natural number
 such that either
such that either
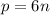 ,
,
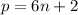 , or
, or
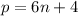 . However,
. However,
- if
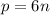 , then
, then
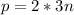 ,
, - if
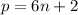 , then
, then
 , and
, and - if
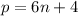 , then
, then
 .
.
By definition of divisibility,
 is divisible by 2. Since
is divisible by 2. Since
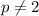 ,
,
 cannot be prime. This contradiction implies
cannot be prime. This contradiction implies
 cannot have a remainder of 0, 2, or 4 when divided by 6.
cannot have a remainder of 0, 2, or 4 when divided by 6.
Case 2: p/6 has remainder 3.
Then there exists some natural number
 such that
such that
 . However, if
. However, if
 , then
, then
 , so
, so
 is divisible by 3. Since
is divisible by 3. Since
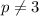 ,
,
 is not prime. This contradiction implies
is not prime. This contradiction implies
 cannot have a remainder of 3 when divided by 6.
cannot have a remainder of 3 when divided by 6.
Therefore, if
 is a prime number such that
is a prime number such that
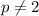 and
and
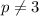 , then when divided by 6,
, then when divided by 6,
 must have a remainder of 1 or 5.
must have a remainder of 1 or 5.
Main proof of no prime trio with common difference of 70.
Check p=2
Consider
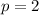 . Then
. Then
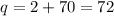 . However,
. However,
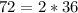 , so
, so
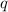 is not prime. Hence,
is not prime. Hence,
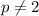 .
.
Check p=3
Consider
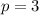 . Then
. Then
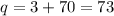 , and
, and
 . However,
. However,
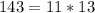 , so
, so
 is not prime. Hence,
is not prime. Hence,
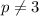 .
.
So, thus far, we've proven that if there is a prime trio with a common difference of 70, that
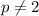 and
and
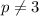 .
.
Proof of the rest of primes by contradiction
By way of contradiction, assume that there does exist some prime trio
 such that
such that
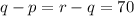 , and
, and
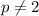 and
and
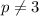 .
.
Then, by the Lemma proven earlier, when
 is divided by 6, it must have a remainder of 1 or 5.
is divided by 6, it must have a remainder of 1 or 5.
Case 1: p/6 has remainder 5
Assume that
 has remainder 5 when divided by 6. Then, there exists some natural number
has remainder 5 when divided by 6. Then, there exists some natural number
 , such that
, such that
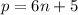 .
.
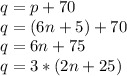
Since
 was a natural number, and the natural numbers are closed over multiplication and addition (meaning, multiplying and adding more natural numbers results in another natural number), then
was a natural number, and the natural numbers are closed over multiplication and addition (meaning, multiplying and adding more natural numbers results in another natural number), then
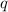 is divisible by 3.
is divisible by 3.
Since
 is prime,
is prime,
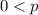 , which implies
, which implies
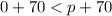
Since
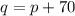 ,
,
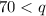 , so
, so
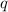 cannot equal 3. Since
cannot equal 3. Since
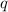 is divisible by 3, but
is divisible by 3, but
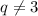 ,
,
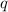 is not prime, which is a contradiction to the existence of this prime trio.
is not prime, which is a contradiction to the existence of this prime trio.
Therefore, either
 cannot have a remainder of 5 when divided by 6, or the prime trio does not exist.
cannot have a remainder of 5 when divided by 6, or the prime trio does not exist.
Case 2: p/6 has remainder 1
Assume that
 has remainder 1 when divided by 6. Then, there exists some natural number
has remainder 1 when divided by 6. Then, there exists some natural number
 , such that
, such that
 .
.
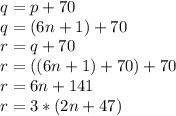
Since
 was a natural number, and the natural numbers are closed over multiplication and addition (meaning, multiplying and adding more natural numbers results in another natural number),
was a natural number, and the natural numbers are closed over multiplication and addition (meaning, multiplying and adding more natural numbers results in another natural number),
 is divisible by 3.
is divisible by 3.
Since
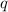 is prime,
is prime,
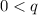 , implying
, implying
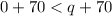 .
.
Since
 , then
, then
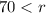 . Therefore,
. Therefore,
 .
.
Since
 is divisible by 3, but
is divisible by 3, but
 ,
,
 is not prime, which is a contradiction to the existence of this prime trio (with a common difference of 70). Therefore, either
is not prime, which is a contradiction to the existence of this prime trio (with a common difference of 70). Therefore, either
 cannot have a remainder of 1 when divided by 6, or the prime trio does not exist.
cannot have a remainder of 1 when divided by 6, or the prime trio does not exist.
Since
 was prime, by our lemma
was prime, by our lemma
 must have either a remainder of 1 or 5. Since both remainder possibilities resulted in a contradiction, our contradiction assumption is false, so there cannot exist a prime trio such that their common difference is 70.
must have either a remainder of 1 or 5. Since both remainder possibilities resulted in a contradiction, our contradiction assumption is false, so there cannot exist a prime trio such that their common difference is 70.