Answer:
D
Explanation:
First let's list down the formulas we will be using.
Area of Quadrant = 1/4 x Area of Circle
=
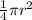
Area of Part of a circle = (θ/360)

First, we will find Angle QOT.
Angle QOT = 360 - 231 = 129
Area of ORST =
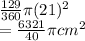
Next we know that, Q is midpoint of OR, therefore OQ = QR
and OQ = 0.5 * OR
OQ = 0.5 * 21 = 10.5cm = radius of Quadrant QOP
Area of Quadrant QOP =
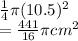
Lastly,
Area of Shaded Region = Area of ORST - Area of Quadrant QOP
=
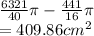
Similar to the other question you asked, choose the closes answer as there might be some rounding differences. I kept it in fractions as it will ensure maximum precision.