Answer:
1) All real numbers n such that

2) All real numbers n such that
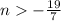
Step-by-step explanation: How did I come up with such answers? Let me show you!
For the first problem, we just solve the inequality easily.
Subtracting 3 from both sides, we get:
4n < 22
Dividing by 4 from both sides, we get:
n < 5.5
Thus, all real numbers n that is less than 5.5 when plugged in for x will be less than 25.
For the next problem, it will be slightly trickier.
Subtracting 5 from both sides, we get:
-7n < 19
Dividing -7 from both sides, we get:
n > -19/7
Did you catch that? We just flipped the inequality sign and turned it from less than to a greater than. Whenever we divide by a negative number, the signs always change.
Thus, for all real numbers n greater than -19/7, when plugging in for x, you will get less than 24.
Hope this helped!