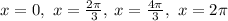Question

Cos(x)=2cos^2(x)-1 0≤x≤2π

Answer 1

`x=0,~x=(2\pi )/(3),\:x=(4\pi )/(3),~x=2\pi`

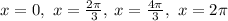
Explanation:

The given equation:

`\cos(x)=2\cos^2(x)-1`

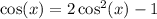
Let
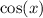`\cos(x)` be
`y`:

`y=2y^2-1`

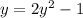
Rewrite as:

`2y^2-y-1=0`

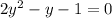
After solving quadratic equation, the solutions are:

`y=1~~~~y=-(1)/(2)`

Substitute back
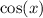`\cos(x)`, it follows:

`\cos(x)=1~~~~\cos(x)=-\frac12`

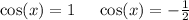
For the first equation, the solution is
`x=0` and
`x=2\pi`.

For the second equation, general solution is:

`x=(2\pi )/(3)+2\pi n,\:x=(4\pi )/(3)+2\pi n`

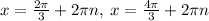
But for the given interval, we must substitute n=0 into the equations so that the values of x must be within interval. Therefore:

`x=(2\pi )/(3),\:x=(4\pi )/(3)`

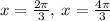
So, the answers are:

`x=0,~x=(2\pi )/(3),\:x=(4\pi )/(3),~x=2\pi`