Question

An icicle with a diameter of 15.5 centimeters at the top, tapers down in the shape of a cone with a length of

350 centimeters.
a. Ice has a density of 0.93 grams per cubic centimeter. Find the mass of the icicle to the nearest gram.
b. On a warm day, the icicle begins to melt. In the first hour, its diameter decreases about 0.7 centimeter in the first hour
and its length decreases by 15 centimeters. How many cubic centimeters of ice melt in the first hour?
c. The icicle's dimensions continue to decrease at a constant rate. A bucket with a diameter of 25 centimeters and a
height of 30 centimeters is placed to catch the water as it drips from the melting icicle. Will the bucket overflow after
the icicle has been melting for 5 hours? Explain. HELP PLEASE

Answer 1

Explanation:

Note: I will leave the answers as fraction and in terms of pi unless the question states rounding conditions to ensure maximum precision.

From the question, we can tell it is a inversed-cone (upside down)

Volume of Cone =
`\pi r^(2) (h)/(3)`

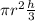
a) Given Diameter , d = 15.5cm and Length , h = 350cm,

we first find the radius.

`r = (d)/(2) \\=(15.5)/(2) \\=7.75cm`

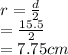
We will now find the volume of the cone.

Volume of cone
`\pi (7.75)^(2) (350)/(3) \\= (168175\pi )/(24)`

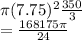
We know the density of ice is 0.93 grams per
`1cm^(3)`

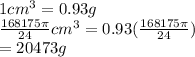`1cm^(3) =0.93g\\(168175\pi )/(24) cm^(3) =0.93((168175\pi )/(24) )\\= 20473 g`(Nearest Gram)

b) After 1 hour, we know that the new radius = 7.75cm - 0.35cm = 7.4cm

and the new length, h = 350cm - 15cm = 335cm

Now we will find the volume of this newly-shaped cone.

Volume of cone =
`\pi (7.4)^(2) (335)/(3) \\= (91723\pi )/(15) cm^(3)`

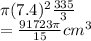
Volume of cone being melted = New Volume - Original volume

=
`(168175\pi )/(24) -(91723\pi )/(15) \\= (35697\pi )/(40) cm^(3)`

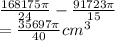
c) Lets take the bucket as a round cylinder.

Given radius of bucket, r = 12.5cm (Half of Diameter) and h , height = 30cm.

Volume of cylinder =
`\pi r^(2) h\\=\pi (12.5)^(2) (30)\\=(9375\pi )/(2) cm^(3)`

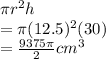
To overflow the bucket, the volume of ice melted must be more than the bucket volume.

Volume of ice melted after 5 hours =
`5((35697\pi )/(40) )\\=(35697\pi )/(8) cm^(3)`

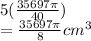
See, from here of course you are unable to tell whether the bucket will overflow as all are in fractions, but fret not, we can just find the difference.

Volume of bucket - Volume of ice melted after 5 hours

=
`(9375\pi )/(2) -(35697\pi )/(8 ) \\=(1803\pi )/(8)cm^(3)`

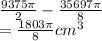
from we can see the bucket can still hold more melted ice even after 5 hours therefore it will not overflow.