Answer:
0.350 (3 d.p.)
Explanation:

Let P(A) = probability that the student is a freshman
Let P(B) = probability that the student owns a credit card
Use the given table to calculate the probability that the student is a freshman:
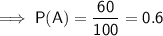
And the probability that the student is a freshman and owns a credit card:
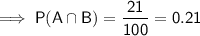
To find the probability that the student owns a credit card given that the they are a freshman, use the conditional probability formula:
Conditional Probability Formula
The probability of B given A is:
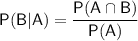
Substitute the found values into the formula:
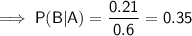
Therefore, the probability that the student owns a credit card given that they are a freshman is 0.35