Question

An approximate solution to an equation is found using this iterative process.

(x₂)³-1
and x₁ = -1
4
Xn+1 =
4/34
a) (i) Work out the value of x₂
(ii) Work out the value of x3
b) Work out the solution to 6 decimal places.

Answer 1

a) i) -0.5

ii) -0.28125

b) -0.254102 (6 d.p.)

Explanation:

Given iteration formula:

`x_(n+1)=(\left(x_n\right)^3-1)/(4) \quad \textsf{and} \quad x_1=-1`

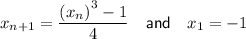
Part (a)(i)

Substitute the value of x₁ into the formula and solve for x₂ :

`\begin{aligned}\implies x_2 & =(\left(x_1\right)^3-1)/(4)\\\\& =(\left(-1\right)^3-1)/(4)\\\\ & = (-1-1)/(4)\\\\ & = (-2)/(4)\\\\ & = -0.5\end{aligned}`

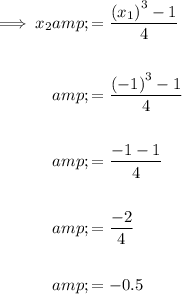
Part (a)(ii)

Substitute the value of x₂ into the formula and solve for x₃ :

`\begin{aligned}\implies x_3 & =(\left(x_2\right)^3-1)/(4)\\\\& =(\left(-0.5\right)^3-1)/(4)\\\\ & = (-0.125-1)/(4)\\\\ & = (-1.125)/(4)\\\\ & = -0.28125\end{aligned}`

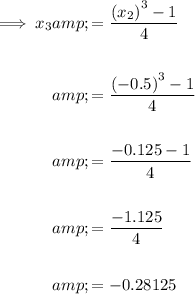
Part (b)

To find the solution to 6 decimal places, keep substituting each new value into the iteration formula until the answers are the same when rounded to the required level of accuracy.

`\implies x_4=-0.2555618286...`

`\implies x_5=-0.2541728038...`

`\implies x_6=-0.2541051331...`

`\implies x_7=-0.2541018552...=-0.254102\:\: \sf (6 \:d.p.)`

`\implies x_8=-0.2541016964...=-0.254102\:\: \sf (6 \:d.p.)`

`\implies x_9=-0.2541016888...=-0.254102\:\: \sf (6 \:d.p.)`

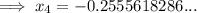
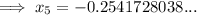
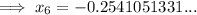
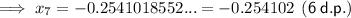
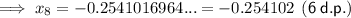
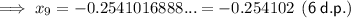
Therefore, the solution is -0.254102 (6 d.p.).