Question

Giving 100 points.

Noah manages a buffet at a local restaurant. He charges $10 for the buffet. On average, 16 customers choose the buffet as their meal every hour. After surveying several customers, Noah has determined that for every $1 increase in the cost of the buffet, the average number of customers who select the buffet will decrease by 2 per hour. The restaurant owner wants the buffet to maintain a minimum revenue of $130 per hour.


Noah wants to model this situation with an inequality and use the model to help him make the best pricing decisions.


1. Write two expressions for this situation, one representing the cost per customer and the other representing the average number of customers. Assume that x represents the number of $1 increases in the cost of the buffet.


2. To calculate the hourly revenue from the buffet after x $1 increases, multiply the price paid by each customer and the average number of customers per hour. Create an inequality in standard form that represents the restaurant owner’s desired revenue.


3. Which possible buffet prices could Noah could charge and still maintain the restaurant owner’s revenue requirements?

Answer 1

1. Cost per customer: 10 + x

Average number of customers: 16 - 2x

`\textsf{2.} \quad -2x^2-4x+160\geq 130`

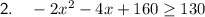
3. $10, $11, $12 and $13

Explanation:

Given information:

• $10 = cost of buffet per customer
• 16 customers choose the buffet per hour
• Every $1 increase in the cost of the buffet = loss of 2 customers per hour
• $130 = minimum revenue needed per hour

Let x = the number of $1 increases in the cost of the buffet

Part 1

Cost per customer: 10 + x

Average number of customers: 16 - 2x

Part 2

The cost per customer multiplied by the number of customers needs to be at least $130. Therefore, we can use the expressions found in part 1 to write the inequality:

`(10 + x)(16 - 2x)\geq 130`

`\implies 160-20x+16x-2x^2\geq 130`

`\implies -2x^2-4x+160\geq 130`

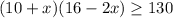
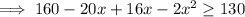
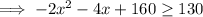
Part 3

To determine the possible buffet prices that Noah could charge and still maintain the restaurant owner's revenue requirements, solve the inequality:

`\implies -2x^2-4x+160\geq 130`

`\implies -2x^2-4x+30\geq 0`

`\implies -2(x^2+2x-15)\geq 0`

`\implies x^2+2x-15\leq 0`

`\implies (x-3)(x+5)\leq 0`

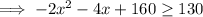
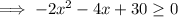
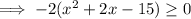
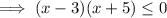
Find the roots by equating to zero:

`\implies (x-3)(x+5)=0`

`x-3=0 \implies x=3`

`x+5=0 \implies x=-5`

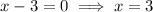
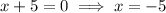
Therefore, the roots are x = 3 and x = -5.

Test the roots by choosing a value between the roots and substituting it into the original inequality:

`\textsf{At }x=2: \quad -2(2)^2-4(2)+160=144`

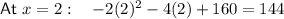
As 144 ≥ 130, the solution to the inequality is between the roots:

-5 ≤ x ≤ 3

To find the range of possible buffet prices Noah could charge and still maintain a minimum revenue of $130, substitute x = 0 and x = 3 into the expression for "cost per customer.

[Please note that we cannot use the negative values of the possible values of x since the question only tells us information about the change in average customers per hour considering an increase in cost. It does not confirm that if the cost is reduced (less than $10) the number of customers increases per hour.]

Cost per customer:

`x =0 \implies 10 + 0=\$10`

`x=3 \implies 10+3=\$13`

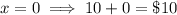
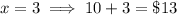
Therefore, the possible buffet prices Noah could charge are:

$10, $11, $12 and $13.